|
Both construction geometry and model geometry can be conceptually separated into
abstractgeometry and
specificgeometry. Abstract geometry is usually broken down into specific geometry. The specific geometry classes are derived from the abstract ones, and thus inherit properties common to all geometry of that type. The specific geometry classes further refine the geometry definition. For example, the abstract geometry for a curve is broken down into specific geometry for specific types of curves, such as ellipse, straight, interpolated curve, etc.
|
|
|
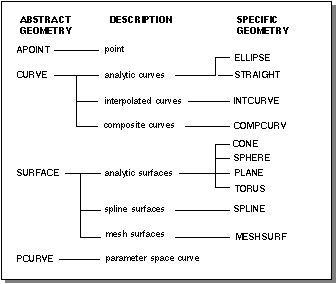
Figure 5-1 uses model geometry classes to illustrates how abstract and specific geometry relate. It shows abstract model geometry on the left and the specific model geometry into which the abstract model geometry is broken down (if any) on the right.
|
|
|
|
|
Figure 5-1. Abstract and Specific Geometry
|
|
|
The abstract model geometry classes
CURVE and
SURFACE define model management related data and methods common to their specific model geometry children classes
CONE,
ELLIPSE,
INTCURVE,
MESHSURF,
PLANE,
SPHERE,
SPLINE,
STRAIGHT, and
TORUS. The abstract model geometry classes
APOINT and
PCURVE do not have specific geometry class children; their geometry definitions are not further refined.
|
|
|
This can be easily seen by looking at the reference template for a given class in online help. The
Derivation field shows the derivation of each class, showing children on the left and ancestors on the right. Children inherit and can use the data and methods of their parents.
|
|
|
Note
|
The model geometry class describing a point is named APOINT to avoid compile and link conflicts with the Microsoft class POINT.
|