|
An
interpolated curve (also known as an
intcurve because of its construction geometry class
intcurve) may represent an intersection between two surfaces, the projection of a curve onto a surface, or any other general curve that is not defined by an explicit equation. An interpolated curve is used for the intersection of two surfaces where there is not a "closed-form" representation available, for exact spline curves, and for silhouette curves.
|
|
|
An interpolated curve, also called an object space curve, is a mapping from an interval of the real line into a 3D real vector space (object space). This mapping is continuous, and one-to-one, except possibly at the ends of the interval whose images may coincide. It must be differentiable twice, and the first derivative must be continuous and non-zero.
|
|
|
If the two ends of the curve are different in object space, the curve is open (refer to Figure 7-1). If they are the same, it is closed. If, in addition, the curve joins itself smoothly, the curve is periodic, with its period being the length of the interval on which it is primarily defined. A periodic curve my be evaluated outside its principal range.
|
|

|
|
|
Figure 7-1. Curve Definitions
|
|
|
Classes
|
|
|
The
intcurve construction geometry class provides an abstraction of the concept of a parametric representation of an interpolated curve. This interpolated curve may be either an exact curve or an approximate (3D B-spline) curve that is a fit to a true curve to within some fit tolerance.
|
|
|
There are two ways to define a 3D B-spline curve:
|
|
|
1.
|
Directly define a curve.
|
|
|
2.
|
Approximate a surface/surface intersection whose primary definition is the surfaces.
|
|
|
Both form part of an
intcurve. The
fit_tolerance (an upper limit on the distance between the true curve and the approximating curve) is zero in the first case, and positive in the second.
|
|
|
The
intcurve class contains a reversed-sense flag and a pointer to another data structure. The flag indicates whether or not the sense of the curve is reversed with respect to the underlying spline. The pointer is to a data structure defined by the
int_cur class (or some class derived from it) and contains the bulk of the information about the curve. This pointer to a separate data structure serves two purposes.
|
|
|
First, when duplicating an
intcurve, the copy simply points to the original
int_cur, thus avoiding copying the bulk of the data. A
use count is maintained in each
int_cur, which allows automatic duplication if modifying a shared
int_cur, and deletion of any
int_cur no longer accessible.
|
|
|
Second, the
int_cur class contains virtual functions to perform all the operations defined for
intcurve that depend on the method of definition of the true curve. New curve types are defined by declaring and implementing derived classes. The
intcurve and everything using it require no changes to utilize the new definition.
|
|
|
The
int_cur class contains the following curve defining information:
|
|

|
A use count indicating the number of times the
int_curve is referred.
|

|
A pointer to a
bs3_curve, which represents a spline approximation to the true curve. Refer to the section
Parameter Space Curves and Surfaces.
|

|
A fitting tolerance representing the precision of the spline approximation to the true curve. This is zero for an exact fit and positive for an approximation.
|

|
Pointers to (up to) two surfaces defining the true curve. A class derived from
int_cur may use these in different ways, but the true curve must lie on each of the non-NULL surfaces, if any. Either or both surface may be
NULL.
|

|
Pointers to 2D parameter space curves with respect to the defining surfaces described above. If the corresponding surface does not exists or is not parametric, this pointer is
NULL.
|
|
|
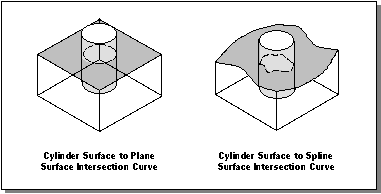
When a surface is intersected with another surface, the intersection routines return an
intcurve as part of the result. This contains the intersection approximated as a 3D parametric curve,
(x,y,z) = F(t), for
a <= t <= b, where
a and
b are the parameter values at the points on the curve corresponding to the ends of the edge. Figure 7-2 illustrates surface/surface intersection curves.
|
|
|
|
|
Figure 7-2. Surface to Surface Intersections
|
|
|
The parameter values are stored in the edge record as
start_param and
end_param for the start and end vertices. If the edge sense is forward along the curve, the edge stores (start_param,
end_param) as (a,
b). If the edge sense is reversed with respect to the curve, the edge stores (start_param,
end_param) as (-b,
-a). Thus,
start_param is less than
end_param in both cases.
|
|
|
If one or both of the surfaces are
splines, the
intcurve also contains one or two 2D parametric curves of the form, (u,v) =
G(t), for
a <= t <= b.
|
|
|
The intersection process produces the information for the 2D and 3D curve(s) at the same time, and so it is convenient to return all the curves in a single
intcurve.
|
|
|
If the fit tolerance is not zero, the
bs3_curve records an approximation to the intersection curve. When necessary, points on the approximate curve are relaxed until they lie on both surfaces (always present). The sense of the
bs3_curve at a point on the curve is in the direction of the cross product
Na x
Nb whereNa and Nb are the normals to the surfaces
a and
b at that point. The
bs2_curves, if present, have the same sense as the
bs3_curve.
|
|
|
If the
fit_tolerance is zero, the
bs3_curve stands alone. It is exact and no surfaces or
bs2_curves are present. This form of
intcurve is useful, for example in a parametric curve associated with an edge of a wire, where the parametric curve has been defined separately--perhaps by specifying the control points of its polygon.
|
|
|
Restrictions
|
|
|
ACIS does not distinguish between the curvatures on either side of a point; therefore, curves used for direct definition (zero-fit tolerance) must have a continuous curvature.
|
|
|
No assumption is made about the relationship between parameter values and object space distances, and parameterization is transformation-independent. However, it is advantageous for the parameterization to be as homogeneous as possible, because various iterative processes are likely to be more reliable and faster.
|