|
The
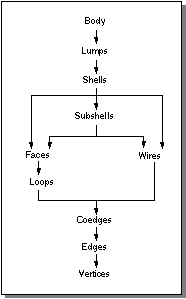
ACIS boundary representation (B-rep) of a model is a hierarchical decomposition of the model's topology:
|
|
|
Body
|
The highest level of model object, and is composed of lumps.
|
|
|
Lump
|
A 1D, 2D, or 3D set of points in space that is disjoint with all other lumps. It is bounded by shells.
|
|
|
Shell
|
A set of connected faces and wires, and can bound the outside of a solid or an internal void (hollow).
Subshells form a further decomposition of shells for internal efficiency purposes.
|
|
|
Face
|
A connected portion of a surface bounded by a set of loops.
|
|
|
Loop
|
A connected series of coedges. Generally, loops are closed, having no actual start or end point.
|
|
|
Wire
|
A connected series of coedges that are not attached to a face.
|
|
|
Coedge
|
Represents the use of an edge by a face. It may also represent the use of an edge by a wire.
|
|
|
Edge
|
A curve bounded by
vertices.
|
|
|
Figure 6-1 shows the relationship of the conceptual topology elements that define the boundary representation of an
ACIS model.
|
|
|
|
|
Figure 6-1. Topology
|
|
|
These elements are implemented in
ACIS using the
C++ classes
BODY,
LUMP,
SHELL,
SUBSHELL,
FACE,
LOOP,
WIRE,
COEDGE,
EDGE, and
VERTEX. Each of these classes is derived from the
ENTITY class. The specific data and methods of each class is described in the class reference template in online help.
|
|
|
The B-rep topology specifies the
hierarchy of elements involved. For example, the topology of a hollow cube would include one body, one lump, two shells (one outside and one forming the inner void), 12 loops, 24 edges, and 16 vertices. It also specifies the
relationships of these elements. For example, the inner void could be centered within the cube, or could be a small rectangular space off to one side. Within these relationships,
transforms mathematically specify relative location, rotation, scaling, reflection, and shear.
|