|
A shell is an entire connected set of faces and/or wires, including connections through a nonmanifold vertex. Faces are connected together along common edges or at common vertices; wires may be connected to faces at end vertices.
|
|
|
A solid block with a dangling sheet is one shell, but a block with a cavity is two shells. A solid block with many embedded faces that are all connected through some path to the exterior faces is one shell, but a solid block with a disconnected "floating" embedded face is two shells (but one lump).
|
|
|
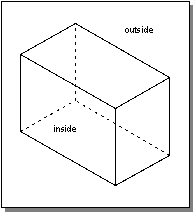
The most common type of shell is made up only of complete, finite single-sided faces (see section
Faces), two of which meet at every edge, with compatible
insides and
outsides. Refer to Figure 6-5.
|
|
|
|
|
Figure 6-5. Complete Shell
|
|
|
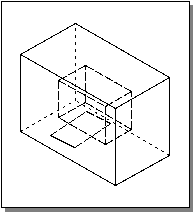
Such a shell divides the whole of space into one finite region and one infinite one. If the finite region is inside the bounding faces, the shell is called
peripheral, otherwise it represents a finite void in an object, and is called
void. Refer to Figure 6-6.
|
|
|
|
|
Figure 6-6. Solid with Void Bounded by One Shell
|
|
|
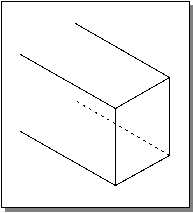
If one or more edges have only one face attached, they are described as
free edges, and the shell is
open. If all the faces are double-sided and all exterior or all interior, then the shell is a double-sided
sheet. If any or all of the faces are single-sided, or there are double-sided faces of both sorts, points in space cannot be classified unambiguously as inside or outside the shell, and it is described as incompletely-bounded, or just
incomplete. Refer to Figure 6-7.
|
|
|
|
|
Figure 6-7. Incomplete Shell
|
|
|
More than two faces may meet along an edge, in which case the edge is said to be nonmanifold. Normally, if one collects together every face at a vertex that can be reached from a given face by crossing one or more edges starting or ending at the vertex, the collection contains all of the faces that meet at that vertex. If this is not the case, the vertex is said to be nonmanifold. One or more wires may be attached to a vertex that is already on the boundary of one or more faces. This again makes the vertex nonmanifold.
|
|
|
A shell that contains any nonmanifold edge or vertex is itself said to be nonmanifold. For these more complex shells, the test for whether they are complete or incomplete is correspondingly more complex. Points in space close to single-sided faces are inside or outside according to which side of the face they are on. Points close to double-sided faces or wire edges are inside or outside, according to whether the face or wire is
interior or
exterior. Any other point is classified the same as another already-classified point, if they can be joined by a continuous path which does not cross any face or wire. If every point in space can be classified unambiguously in this way, then the shell is complete; otherwise, it is incomplete. Any shell which contains a single-sided face with a free edge is automatically incomplete.
|
|
|
Bodies containing incomplete shells may only participate in modeling operations in regions where their shells are defined. Even then, some configurations give rise to ambiguous results, and so are disallowed.
|