|
A loop represents a connected portion of the boundary of a face. It consists of a set of coedges linked in a doubly-linked chain which may be
circular or
open-ended.
|
|
|
If either end of an open-ended loop is at a finite point, then the face containing the loop is necessarily
incomplete. If either end is at infinity, then the face is
infinite.
|
|
|
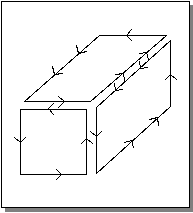
The illustration in Figure 6-11 contains three closed loops. Each loop is the boundary of a complete, finite face. In the actual physical structure, the adjacent parallel lines are coincident.
|
|
|
|
|
Figure 6-11. Loops of Edges
|