|
An edge is the topology associated with a curve. The direction of an edge can be either the same direction as its underlying curve, or it can be the opposite direction. If it is the same as the curve direction, the edge's
sense relative to the underlying curve is
forward; otherwise, its sense is
reversed. Each edge contains a record of its sense relative to its underlying curve.
|
|
|
An edge is bounded by one or more vertices, referring to one vertex at each end. If the reference at either or both ends is
NULL, the edge is
unbounded in that direction. If the underlying curve is
infinite, so is the unbounded edge. When the curve is closed, the vertex references must both be the same or both
NULL. If both vertex references are
NULL, the edge is the whole curve; unless the curve is open and bounded, in which case the vertices must coincide with the curve ends.
|
|
|
A special case occurs when the geometry pointer is
NULL and both vertex pointers point to the same vertex; for example, at the apex of a cone. Few
ACIS operations work correctly with edges that have one or both end vertex pointers
NULL.
|
|
|
An important feature of
ACIS edge representation is the arrangement of the coedges around an edge. (Refer to section
Coedges in this chapter for more information.) If only two faces meet at an edge, the two coedges from those faces point to each other through the coedge partner pointers. (If there is only one coedge, its partner pointer is
NULL.) If more than two faces meet at an edge, the coedges are in a circular linked list. The order of the list is important, because it represents the
radial ordering of the faces about the edge in a counterclockwise direction. Figure 6-15 shows a sheet body that contains a nonmanifold (more than two faces incident) edge. The edge is directed such that it is coming toward the reader, and the coedges are ordered counterclockwise about it in the partner list as indicated by the arrow.
|
|

|
|
|
Figure 6-15. Radial Coedge Ordering
|
|
|
The purpose of radial coedge ordering becomes clear during traversal of an
ACIS model that contains faces embedded with a solid region, such as in a 3D finite element model. Moving from a face across an edge to the radially closest adjacent face is a simple list operation, rather than a geometric operation as when coedges are not ordered. For example, moving to the face that is closest to the front (outward normal) side of a face is done by moving to the next partner pointer, if the original face coedge is
FORWARD. If the original face coedge is
REVERSED, moving to the closet face is done by moving to the previous partner pointer (obtained by walking all the way around the list).
|
|
|
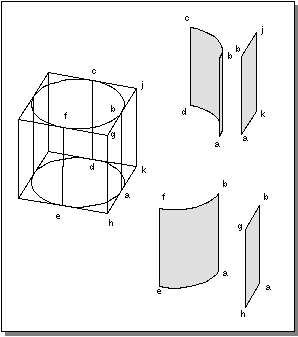
In a nonmanifold body shell, the edge may be adjacent to more than two faces. A nonmanifold body is shown in Figure 6-16. An edge common to four faces is at each point where the cylinder is tangent to the outside edge of the block. In the example, edge
ab is common to two faces on the inside wall of the cylinder (abcd and
abfe) and two faces on the outside of the block (abgh and
abjk). Edge
ab is common to all four faces. When there are more than two coedges associated with an edge, they are ordered counterclockwise about the edge.
|
|
|
|
|
Figure 6-16. Nonmanifold Body With Common Edge
|